Mastering the Art of Completing the Square: A Step-by-Step Guide
Completing the square is a powerful algebraic technique used to solve quadratic equations, reformat expressions, and analyze graphs. Whether you’re a student or a math enthusiast, understanding this method can enhance your problem-solving skills and deepen your comprehension of algebraic concepts.
Key Takeaways
- Completing the square is essential for solving quadratic equations and converting them into a form that reveals their properties.
- This technique is invaluable for graphing parabolas and understanding their vertex form.
- Mastering this method can simplify complex algebraic problems and boost your confidence in mathematics.

Understanding the Concept of Completing the Square
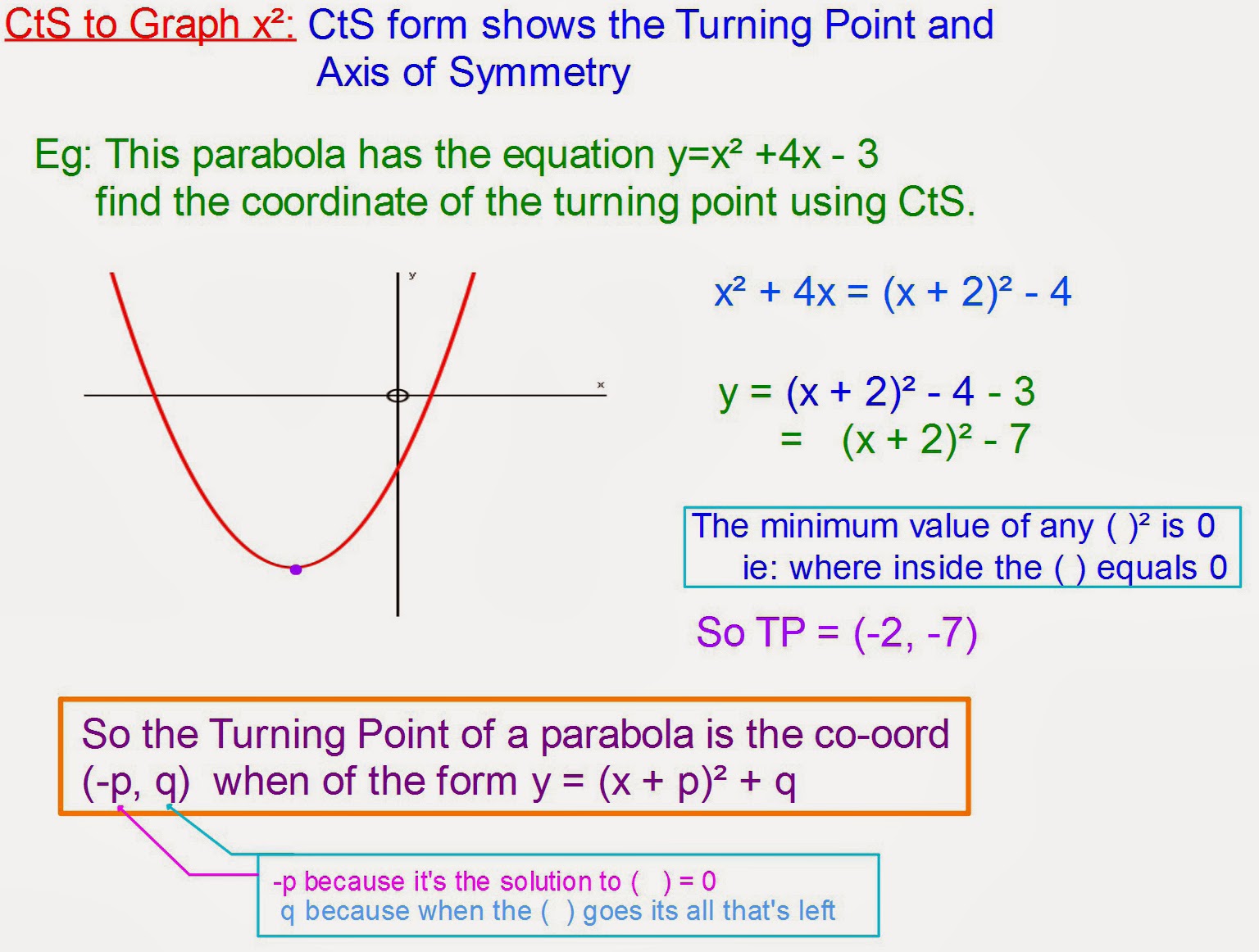
Before diving into the process, it’s crucial to grasp what “completing the square” means. In algebra, this technique involves transforming a quadratic expression into a perfect square trinomial. This form is particularly useful because it makes solving equations and graphing functions more straightforward.
Why is Completing the Square Important?
Completing the square is not just an academic exercise; it has practical applications in various fields. Here are a few reasons why mastering this technique is beneficial:
- Simplifies Quadratic Equations: By converting a quadratic equation into a perfect square trinomial, you can easily find the roots of the equation.
- Facilitates Graphing: The vertex form of a quadratic equation, obtained through completing the square, makes it easier to graph parabolas.
- Enhances Problem-Solving Skills: Understanding this technique can improve your overall algebraic skills and problem-solving abilities.
The Step-by-Step Process of Completing the Square
Let’s break down the process of completing the square with a clear, step-by-step guide:
Step 1: Start with a Quadratic Equation
Consider a standard quadratic equation in the form ax² + bx + c = 0. For simplicity, let’s work with an equation where a = 1, such as x² + bx + c = 0.
Step 2: Move the Constant Term
Rearrange the equation to isolate the constant term on one side. For example, if you have x² + 6x + 8 = 0, rewrite it as x² + 6x = -8.
Step 3: Complete the Square
To complete the square, you need to add and subtract the square of half the coefficient of x from both sides. For x² + 6x, half of 6 is 3, and 3 squared is 9. Add and subtract 9:
x² + 6x + 9 = -8 + 9
This simplifies to:
(x + 3)² = 1

Step 4: Solve the Equation

Now that you have a perfect square trinomial, you can solve for x by taking the square root of both sides:
x + 3 = ±√1
Therefore, x = -3 ± 1, which gives you the solutions x = -2 and x = -4.
Applications of Completing the Square

Completing the square is not limited to solving quadratic equations. It has several other applications:
Graphing Parabolas
By converting a quadratic equation into vertex form, y = a(x-h)² + k, you can easily identify the vertex of the parabola, which is the point (h, k). This form makes graphing more intuitive and helps in understanding the parabola’s orientation and width.
Deriving the Quadratic Formula
The quadratic formula, x = [-b ± √(b²-4ac)]/(2a), can be derived using the method of completing the square. This derivation is a testament to the versatility and importance of this technique in algebra.
Solving Real-World Problems
Completing the square is also used in physics and engineering to solve problems involving projectile motion and optimization. Understanding this method can thus have practical implications beyond the classroom.
Tips for Mastering Completing the Square
Here are some tips to help you master this technique:
- Practice Regularly: Like any mathematical skill, practice is key. Work on various problems to become proficient in completing the square.
- Understand the Logic: Instead of memorizing steps, focus on understanding the logic behind each step. This will make it easier to apply the technique to different problems.
- Use Visual Aids: Drawing graphs and visualizing the transformation of the equation can help solidify your understanding.
Completing the square is a fundamental algebraic technique that offers numerous benefits, from simplifying equations to enhancing your problem-solving skills. By mastering this method, you can tackle a wide range of mathematical challenges with confidence and precision. Whether you’re preparing for exams or exploring advanced mathematical concepts, this skill is an invaluable addition to your toolkit.




